Valve Tuning Theory — Tiffany Johns

There is a small tuba-oriented website that offers a fascinating valve tuning/fingering calculator for download. It will take the valve tubing lengths (as proportional to the overall length of the instrument) you input and spit out every possible fingering, what pitch would result, and how close to in tune that pitch would be. As someone who enjoys brass instruments, numbers, and spreadsheets, I had to download it right away. Since then, I’ve spent many hours trying countless theoretical valve combinations and recording the results. I would hate for my findings to only exist in my downloaded copy of an Excel spreadsheet, so here we are.

It is important to clarify that the calculator only models the 2nd partial, as it was designed originally to figure out what valve lengths work best for low register intonation on tuba. On a real instrument, if the tubing is cut to the correct length the modeled tuning tendencies will also be correct. However, this accounts only for that 2nd partial, and all brass instruments have partials less in tune than others. So things like the viability of alternate fingerings in the upper register can’t be predicted. Additionally, all brass instruments have a zone in which the note you’re aiming for locks in, called a “slot”, rather than fixed points at which each note sits. It is still up to the player to tune the instrument and individual valves properly, and then hit the center of the slots to play in tune.

That said, a theoretically-perfect valve configuration will make the player’s job much easier, and eliminate the need to manipulate valve slides while playing or lip out-of-tune valve combinations into tune. Thus the goal for fully-chromatic instrument is to find a configuration where every note in the 2nd partial all the way down to (at least) the note a half-step above the 1st partial fundamental is as close to perfectly in tune as possible. On a 9’ tenor B-flat instrument such as euphonium, this means Bb2 down to B1 (with Bb1 being the fundamental). Of course, fingerings will also work the same in higher partials, with the player only having to compensate for the individual instrument’s partial quirks. (Typically: 3rd partial slightly sharp, 6th partial very sharp, 7th partial unusably flat. The other partials vary more between individual instrument models, such as the 5th partial being flat on some trombones and sharp on others.)

It is also important to clarify that on some instruments, especially smaller ones like trumpets, it is often much more practical to have a slide kicker or two than have a totally different valve system. This is why the standard 3 valves are so ideal on trumpet and flugelhorn, despite being a very imperfect configuration in the absence of slide kickers/triggers. But for large instruments like tubas, getting the valve configuration as close to as perfect without manipulation is more valuable.

Let’s start with six valves. The obvious disadvantage to six valves is that you have a lot of valves to work with. Not every instrument will have room for them, and of course more valves = more cost. However, six valves provide multiple near-perfect configurations that any fewer valves cannot match.

The first and most logical system is the standard 6-valve setup. This is the setup seen on all modern 6-valve F tubas, and consists of 3 normal valves (whole step, half step, 1.5 steps), normal 4th valve (perfect 4th), a long whole step 5th valve, and a long half step 6th valve. (A "long step” is one that is in tune with the 4th valve down. So on a B-flat instrument, a long whole step would be a whole step in F.) When plugged into the calculator, the most optimal fingerings end up as follows:

For everything in this calculator, I set it to a 9’ B-flat instrument such as euphonium, as that is what I am the most familiar with. Additionally, the 3rd valve is always tuned for 2-3 to be in tune (slightly lower than tuning to just 3) except where noted.

I was most concerned about the 4th valve register, as the first 3 valves are a known entity and work well enough. They aren’t perfectly in tune, but brass players are used to compensating for that. So, although the calculator spits out every possible fingering starting at the first note below the open 2nd partial (in this case A2) and goes down as far as the valves will take it, I only input the optimal 4th valve register results for the sake of clarity. These are not the ONLY possible fingerings, but the most in-tune. The left column shows the note, the right column shows the fingering, and the middle column shows how close to in tune that fingering is. “9-” means the note is 9 cents flat, while “1+” means it’s 1 cent sharp. For reference, the standard 1-2 fingering is 10 cents sharp, so these are all well within acceptable deviation. Not perfect, but close enough. Adding up all of the middle column (in tune = 0) gives a deviation score of 19.

As if it wasn’t already not good enough, you can further optimize this configuration. By shortening the long half step 6th valve by about 1.39”/35.39mm so that 13456 is in tune, you get the following beautiful result:

This has a deviation score of just 7 and is the closest to perfection that I have found. It requires no new fingerings and is so close that it might as well be perfect. You could even make the 6th valve dependent on the 4th or the 1st if you wanted.

To be frank, you could stop reading here if you just wanted to grab the best solution and run. It’s already standard, it’s near-perfect, it just works. But we’re just getting started!

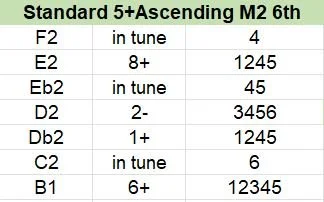
The next 6-valve configuration we’ll look at is one of my favorites.

This configuration uses the same first 5 valves as the standard 6-valve arrangement, but the 6th valve is an ascending whole step. Ascending valves are relatively rare, but can be very useful. Although less familiar than the unoptimized standard 6-valve setup, this setup scores a slightly better deviation score of 17.

Now, if you have an instrument that you want to punch well above its weight (or more accurately length) in terms of low-end prowess, it turns out the old French tuba in C (as written for in Ravel’s famous orchestration of Pictures at an Exhibition) had a very competent valve system for doing just that. Taking that template and updating it to use a modern 3rd valve (1.5-step instead of the old 2-step), and you get the following:

To clarify, this configuration includes 4 normal valves, a long half step 5th valve, and a perfect-5th 6th valve. Apart from the 1.5-step 3rd valve, it is the same as the original French instruments. As you can see, it takes you far lower than a modern 6 valve setup could, thanks to the quint valve. It’s not the most in tune in that pedal-replacement register, but we can improve that by making the 5th valve a long whole step instead of a long half step, thereby resulting in a standard 5-valve configuration plus the P5 6th valve:

While neither of these setups are as ideal as the standard 6-valve setup, higher-pitched instruments intended to still be able to play commandingly down to the pedal register and below could benefit from such a setup. The Half-Modern setup (long half step 5th) works better above the bonus pedal-replacement register, with a deviation score of 16 above Bb1, while the Modern setup (long whole step 5th) works better in the bonus pedal-replacement register but significantly worse above it (scoring a deviation score of 26). Still, even 26 is very usable in the real world.

These four configurations are the only ones that I classified as optimal, denoted by the green background underneath the configuration name. Any of them would be an excellent choice. There were unsurprisingly some excellent 7-valve configurations, but they didn’t provide any real advantage over the best 6-valve setups so I didn’t consider them optimal. Here are most of the other 4, 5, 6, and 7 valve configurations I tested and their derivation scores (all ignoring any bonus pedal-replacement notes):

Modern French Tuba 6 with ascending whole step 3rd valve (a la true French double horns): 26 (great except for D2, at 17 cents sharp)
Standard 6+Long 1.5-step 7th (aka 3 normal valves, normal 4th, and 3 long valves in tune at the length of the 4th valve; functions the same as a full double instrument but with more fingering possibilities): 9 (almost perfect, but…the optimized standard 6 is even better with one fewer valve. Still, if you have 7 valves lying around…)
3+3 (3 normal valves, 3 long valves; aka the setup above but without the 4th valve): 45
Modern French Tuba 6+ascending whole step 7th: 13 (SO not worth the trouble)
Modern French Tuba 6 with ascending whole step 5th: 15
Modern French Tuba 6+long half step 7th, tritone 7th, or Major 3rd 7th: they became clear it was so not worth it I didn’t even progress far enough to get a derivation score
Standard 5 valves (long whole step 5th): 48
Standard 5 with ascending whole step 3rd: 38
Standard 4 valves: 77 (and that’s not including the non-existent low B and so-bad-it-might-as-well-be-non-existent low C!)
Standard 4 with ascending whole step 3rd: 41 (no low D or Db)
Standard 4+perfect-5th 5th valve: 59
Standard 4+ascending whole step 5th: 66
Standard 4+tritone 5th: 65
Standard 4+Major 3rd 5th (2 whole steps): 96
Standard 3+P5 4th+ascending 5th: 54
Standard 3+tritone 4th+ascending 5th: 50
Standard 3+Major 3rd 4th+ascending 5th: 87
Standard 3+tritone 4th: 88 (…and still no low B)

The moral of the story is that I couldn’t find a single configuration with less than 6 valves that was any good. The standard 5-valve setup with the long whole step 5th was the best of the lot, but still several dimensions behind any of the good 6-valve setups. The situation with only 4 valves was even more dire. Regarding possible 4 to 7 valve configurations starting with the normal first 3 valves, I think we can pretty safely close the book with our knowledge of the Four Good Tunings™.

…however…

…what if you DON’T start with the normal first 3 valves?

While pondering what one could do with a 2-valve G bugle to make it fully chromatic in a way that’s not annoying, I had an idea and spontaneously invented a beautiful 2+2 valve system that has the same range as a normal 3 valves and eliminates the need for any slide kickers or adjustment.

First, let’s take a look at the standard 3 valves for comparison. When the 3rd valve is tuned to 2-3, you have 0, 2, and 1 in tune, 12 at 10 cents sharp, 3 at 16 cents flat, 4 in tune, 13 at 15 cents sharp, and 123 at 38 cents sharp. It is hardly a good system on paper, with a derivation score within that partial of 79. Of course, kickers solve all of this…but not every instrument has room (physically or ergonomically) for even one kicker.

My 2+2 system works as follows. The first two valves are your standard 2 valves (whole step and half step), as found on any 3 valve set with the 3rd valve ignored, or any 2-piston G bugle. The next two valves are also a whole and half step to start, but tuned very specifically. The third valve is tuned so that 123 = an in-tune 1+3 fingering on a normal valve set. This means lengthening the slide from its standard whole step position by about 3.22”/81.75mm on a 9’ B-flat instrument. The fourth valve is tuned so that 124 = an in-tune 2+3 fingering on a normal valve set. This means lengthening the slide from its standard whole step position by about 1.93”/49.10mm on a 9’ B-flat instrument.

The result?

A derivation score of 12.

Additionally, 2-valve G bugles have a kicker on the 1st valve slide that kicks inward, in order to bring the 7th partial 1st-valve note (which is extremely flat, and able to be completely avoided on 3-valve instruments) up to pitch. Given as the 2+2 configuration was designed specifically for 2-valve G bugle valve sets that would otherwise be useless, it is likely then that a 2+2 instrument would have at least one inward kicker on the 1st valve. On the data above, 1+2 is listed as the fingering for G2 because it is the closest to being in tune. As it is sharp and not flat, an inward kicker wouldn’t help. However, 1+4 is another available fingering, which is 16 cents flat. The inward kicker, long enough to bring a note a full quarter step flat into tune, would undoubtedly be able to bring that 1+4 fingering up to pitch.

Having this 2+2 valve block as a base opens up another world of possibilities with additional valves. So far I have run through 15 configurations with 6 valves (2+2+2?), and while none are perfect, nearly all of them are very good and several are among the closest to perfection of any configuration I’ve found thus far.

Of course, none of those configurations is that practical. Even just the 2+2 system requires learning a new fingering pattern, even though it is arguably more logical than the usual 3 valve pattern. The basic pattern of the left hand 3rd and 4th valve is identical to the right hand 1st and 2nd. But the 2+2 system is only worth doing over a standard valve set in a very specific circumstance involving 2-piston G bugles.

What makes it even more viable for that context is that the 3rd and 4th valves can be made dependent of the 1st and 2nd. Since every standard fingering involving 3 or 4 has both 1 and 2 down, 3 and 4 can be inset in those valves’ tubing. What this means is that you could set both valves in alternate slides that plug in to the existing valves’ valve slides, without modifying the original bugle in any way. And because the valves are dependent, the bugle would feel exactly the same to play until you used one of the additional valves.

Eventually, I would love to be able to 3D-print 2-valve sets for G bugles and sell them so that players could slot them into their 2-valve bugles whenever they needed the missing pitches. A +2 valve set would drastically expand the musical possibilities of a 2-valve bugle, and would do so without altering the original instrument in any way. What’s not to like?